full credits: DATAROOM del Corriere della Sera
Fabbriche di elettrodomestici, mobili, alimentari, automobili, a singhiozzo si stanno fermando tutte. Proprio ora che riparte la domanda. La questione è che pressoché tutte le materie prime sono diventate introvabili e costosissime. Gli inglesi la chiamano everything bubble: la bolla sui prezzi di qualunque cosa. Per un Paese trasformatore come l’Italia, che deve importare quasi tutto, sta diventando un problema serio. Quanto sta accadendo è il risultato di tre fattori che si sommano: reali, finanziari e logistici.
Partiamo da quelli reali. Nei primi mesi della pandemia i valori dei prezzi delle materie prime sono crollati del 20-30%. La Cina, che ha un’economia pianificata, ne ha subito approfittato per fare scorte, avvantaggiata anche dal fatto di essere ripartita con quattro mesi di anticipo. Ma subito dopo i prezzi hanno ricominciato a salire, e ora sono alle stelle, perché tutti i Paesi sono ripartiti di scatto, con i magazzini di ogni continente vuoti per colpa dell’organizzazione just in time (le imprese si sono abituate, per essere più efficienti, a non accumulare scorte) e, quindi, adesso vanno riempiti da zero. Poi ci sono cause che hanno a che fare con i mercati finanziari. Le materie prime sono diventate un investimento interessante perché sono prezzate in dollari, moneta debole in questo momento, quindi sono convenienti per chi le acquista in euro o altre valute. Inoltre: investire in titoli di Stato dà rendimenti bassissimi, quindi tanto vale mettere soldi in materie prime e sui titoli derivati a esse legati. A tutto questo bisogna aggiungere gli aspetti logistici come l’aumento a dismisura dei costi di trasporto. Il Dry Baltic Index, indice che sintetizza gli oneri di nolo marittimo per prodotti secchi e sfusi (minerali, cereali, eccetera), ha registrato nell’ultimo anno un +605%. Tra le cause anche l’introduzione del nuovo regolamento approvato dall’Organizzazione marittima internazionale che impone a tutte le navi di abbassare la quota di zolfo nell’olio combustibile: dal 3,5% (massa per massa) dal gennaio 2020 si passati allo 0,5%. Questo cambiamento ha comportato la rottamazione di parte delle navi e revamping di altre, anche per le navi portacontainer e portarinfuse che trasportano merci dalle Americhe, dall’Africa, dall’Asia e dall’Australia, e il costo si è scaricato sui prezzi.
Ci sono alcune materie prime necessarie in quantità mai utilizzate finora, perché sono indispensabili alle due rivoluzioni in corso nel sistema produttivo: la transizione green e quella digitale. Parliamo di rame, litio, silicio, cobalto, terre rare, nickel, stagno, zinco. I più lungimiranti sono stati i cinesi. A casa loro sono grandi estrattori di rame, litio, terre rare. E quello che gli manca se lo vanno prendere nei Paesi produttori: il nichel nelle Filippine e in Indonesia, in Congo possiedono le principali miniere di cobalto. Minerali che poi trasformano direttamente nella madre patria. Secondo Benchmark Mineral Intelligence, società di analisi britannica, l’80% dei materiali grezzi necessari per la costruzione delle batterie agli ioni di litio proviene da aziende cinesi. Per l’approvvigionamento di terre rare dipendiamo dalla Cina per il 98%, idem per il borato dalla Turchia, dal Sud Africa per il 71% del fabbisogno di platino. Secondo le stime della Commissione, per le batterie dei veicoli elettrici e lo stoccaggio dell’energia nel 2030 l’Ue avrà bisogno di un approvvigionamento di litio fino a 18 volte superiore a quello attuale, e 5 volte di cobalto. Quantità che triplicheranno nel 2050, mentre decuplicherà la domanda di terre rare utilizzate nei magneti permanenti (veicoli elettrici, tecnologie digitali, generatori eolici).
Con vent’anni di ritardo rispetto alla Cina, lo scorso ottobre l’Unione Europea ha costituito l’Alleanza per le materie prime. La strategia è quella di diventare più autonomi puntando su tre obiettivi:
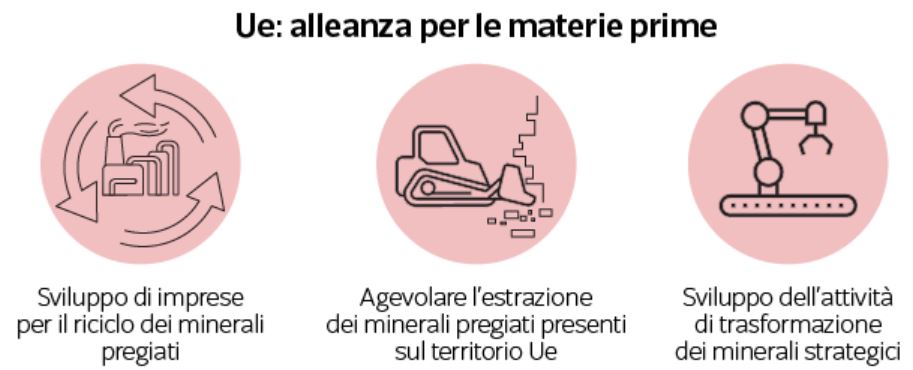
1: favorire l’attività estrattiva dei metalli presenti sul territorio europeo utilizzando tecnologie avanzate. La domanda di litio, per esempio, può essere soddisfatta internamente per l’80% entro il 2025. Oggi i metalli strategici estratti in Europa, come il litio, vengono poi trasformati principalmente in Cina. Il processo di lavorazione andrà invece sviluppato rapidamente a casa nostra. Sono stati creati sei centri d’innovazione, di cui uno a Roma, con lo scopo di implementare il settore creando partnership tra imprese e tra imprese e università. In Italia abbiamo un po’ di cobalto in Sardegna e a Punta Corna, in Piemonte, dove si trova anche il nichel; mentre a Gorco, in provincia di Bergamo, c’è lo zinco. Certo, si tratta di attività invasive. Ma andrà deciso una volta per tutte se lasciarle nelle mani di Paesi che, oltre a renderci dipendenti economicamente ed esposti ai ricatti dei prezzi, hanno regole meno rigorose delle nostre e utilizzano tecnologie più inquinanti.
2: potenziare l’attività di riciclo dei metalli pregiati. Abbiamo dimostrato di saperlo fare con carta e alluminio, ma non con i rifiuti elettronici, a partire dalle batterie dei cellulari. Per quel che riguarda il riciclo delle batterie, mandiamo il grosso in Cina, che ormai domina il mercato mondiale, e la paghiamo svolgere questo tipo di attività. Poi dalla Cina compriamo le batterie nuove e buonanotte. Un minerale strategico è il cobalto. Dai dati dello European Institute of Innovation Tecnology Rowmaterials: l’Ue paga per importarne 40.000 tonnellate ogni anno, la metà finiscono in prodotti che restano all’interno della Ue, dove il riciclo a fine vita però è minimo, quando invece una percentuale che può sfiorare il 50% è recuperabile. Inoltre andiamo a buttare migliaia di tonnellate di computer e telefonini usati nelle discariche di casa nostra e in Africa. Un comportamento irresponsabile che, da un lato, provoca un inquinamento gigantesco e, dall’altro, deturpa l’ambiente perché rende necessario estrarre nuovo cobalto. Per questo si dovrà puntare su filiere di raccolta, stoccaggio e riciclo, che oggi mancano completamente.
3: costruire una politica estera e industriale comune per ottenere le concessioni dei minerali che non abbiamo. Sicomines, un consorzio di società statali cinesi, nel 2008 ha firmato un accordo con il Congo per diritti di estrazione di rame e cobalto fino al 2033, per un valore stimato in 84 miliardi di dollari. In cambio si è impegnata a investire 6 miliardi di dollari nelle infrastrutture del Paese e circa 3 miliardi nel settore minerario. Da anni in quelle miniere è scandalosamente sfruttato il lavoro dei bambini, provocando l’indignazione di mezzo mondo. Offrire condizioni migliori non è solo una necessità. È un dovere.